Will smart balloons change design?

At the 2009 ACADIA (Assoc. for CAD In Architecture) conference, I was blown away by all the radical design ideas brought forth. Of them, the most intriguing ideas imagined how new technologies could be used to create responsive structures - buildings that could change shape and function in reaction to external stimuli. Ideas like this are more familiar in the robotics field, but it turns out that simple mechanisms can be utilized to bring our buildings alive.

Mehran Gharleghi and his colleagues at Studio Integrate in London have been exploring the field of responsive structures. Their motivation was to apply simple light weight technologies to provide naturally ventilated and cooled spaces in hot sunny locations. The following is a short description of their research on an Adaptive Pneus in their own words:

"This research focuses on the performative capacities of a pneumatic material system in regard to the specific environmental conditions. It explores a new approach that integrates form generation, material behavior and capacity, manufacturing, and assembly to deliver a modulated environment suitable for occupation.

The focus of the design process and research was the use of Adaptation as a mechanism to modulate environmental performance. Here, adaptability relates to the responsive action that affects the performance of the whole building and, therefore, holds a much closer relationship to the biological and natural ideas of responsiveness.

Location of the sun during the day acts as a trigger to adapt the system, allowing the system to augment passively the environmental conditions. Detection and reaction are embedded in each cell, and responses take place locally and independently. These responses at the regional and global scales allow for the distribution of intelligence across the whole system."

Will a catenary span 600 ft?

The Chameleon is a design concept for linking Chicago’s Northerly Island to the shore near Soldier field. In the second part of my series exploring the potential structure of this design, I applied basic load and deflection principles to estimate a steel quantity. Unsatisfied with the brute force approach, I explored other structural forms and became intrigued by the concept of the catenary.

A catenary is the theoretical shape that a hanging chain or cable will assume when acted on only by its own weight. Such a member experiences only tension forces and is very efficient for spanning a distance. The inverse would be the classical arch, a design feature that ideally only experiences compression. Both structural concepts were widely implemented until the advent of steel beams. In fact, the Catalan architect Antoni Gaudi was known to utilize catenary models in his most famous works. A series of strings was used to construct the complex arch and vault system he desired - just upside down. Gaudi realized the relationship between strings in pure tension and stones in pure compression, a law most eloquently described by Newton. “To every action there is an equal and opposite reaction.”

The arc of the catenary is defined by a fairly simple mathematical relationship. y=a*cosh(x/a) The key constant in the equation, “a,” represents a relationship between the tensile force in the member and the applied gravitational force. By tuning the axial stiffness, or resistance to elongation, and strength of the members the arc can be adjusted. Even within fairly rigid confines, such as those set by the need to allow boats to pass beneath the bridge, a satisfactory geometry can be achieved.

Recently building engineers have begun to revisit the potential of catenary action. Many of the most recent reports have dealt with the capacity for floor systems to apply catenary effects to prevent progressive collapse. If properly detailed, the floor beams on several floors can actually form a catenary that will support a column despite the removal of a column support. These recent reports still caution that the method is only effective when large deformations occur and the system has a substantial span to depth ratio. Fortunately, both of these conditions may be permitted in our long span bridge design.

Several bridge forms that utilize this structural technique. Simple rope bridges, like those creaky death traps featured on Indiana Jones, are the most elementary catenary structure. Unlike a conventional suspension bridge, these parabolic structures follow a true catenary curve, because the flexible deck follows the free hang of the cable. The longest such rope bridge, located near Vancouver, is an incredible 450 ft. long. Of course, the problem with these true catenary structures is the bounce and sway experienced by the brave souls that cross them.

Hybrid applications of the catenary shape have been applied in more static conditions. While the cable of a suspension bridge may initially follow a catenary arc, once the deck cables are attached, the form becomes a parabola carefully computed by the designers. Nor is it essential to use cables to achieve the purpose. Tower Bridge, in London, is known as a suspension bridge, but the “cables” are actually riveted steel plate sections. Therefore, we can assume that a catenary form can be applied to a solid static form.

The major implicit challenges are tuning the member sizes to achieve the final elongated position and constructing given the daily changing member orientations (as construction load is applied). Such a non-linear analysis and sequencing model is beyond the scope of this speculative blog. However, if we overlay a tension catenary (blue) and a compression arch (red) on the elevation of the bridge, we can see potential in the architectural form. Two more parabolic lines (green) appear to close the gaps, facilitating a continuous structure. Even if the intent of the exterior surface is to be undulating and unpredictable, we could envision facet lines that follow the main structural form or find ways to embed that within the structure. I believe this is a concept that brings structural harmony and simplification to a chaotic form that is more visually indicative of the sense of turbulent times.

Taking the catenary concept one step further, I would further propose that the interior pedestrian paths be supported by the means of one massive catenary bridge. Spanning 600 ft., it would be the longest “rope bridge” in the world. Far from typical, this catenary bridge would be comprised of dual layers with a depth of 16 ft. between. Ramps would connect the two layers and provide exit from the top down to dry land. The original programming called for entertainment and snack bar venues. Providing a stable surface, not wildly influenced by passing pedestrians would be challenging. Perhaps, the catenary pedestrian bridge could be connected to the exterior structure via a system of dampers, to modulate the movement and sway.

Though the initial design suggests that the pedestrian walks be suspended from the super structure, the incorporation of a pedestrian catenary bridge might provide the necessary construction platform to facilitate the building of the shell structure. At times during construction, might the shell actually be suspended from the pedestrian bridge. This might be a significant design consideration that has greater bearing in determining the size of the catenary bridge members than the actual person load.

Though this analysis has been brief, I hope it has accurately represented the thought process of an engineer presented with a design challenge. Use of catenary and arch forms is far from new technology, but they may be appropriate for this project. Even within an apparently static form, there might be potential to implement a bridge form known in the popular mindset as awkwardly unstable. From a structural dreamer’s standpoint the irony of the design is quite satisfying. Delivering a record setting structure goes even further in achieving the goal of a landmark bridge.

What other examples of catenary bridges are out there? Does the catenary concept have merit? Do you think the pedestrian platform would be steady enough to be comfortable? How might contractors cope with the gradual change in shape that will occur in the structure throughout construction? Comment below.

Will a bridge link Northerly Island?

The Chameleon pedestrian bridge would link Soldier Field to Northery Island. But, will it stand? In this blog, I will apply basic structural principles and equations to estimate the material requirements of such a bridge. To the greatest extent possible, I have tried to remain true to the original design intent, but early schematic evaluations require lots of approximation.

My first caveat is that I’m a building engineer. The layman would be surprised at the differences between the thought processes and building codes that apply to bridges and buildings. However, given the functional intent of this pedestrian bridge, it might is some senses be better treated as a building. To that end, I’ve used the Chicago Building Code (CBC) as a baseline for determining load conditions and general requirements. As we proceed, though, you may find that more elements of common vehicle bridges will find their way into the concept by way of seeking the most efficient forms.

As a building engineer, my first inclination was to evaluate the bridge concept as a beam. In the classic, simply supported beam, the greatest bulk of the structure would necessarily need to be located in the center of the span. However, the architectural intent is to minimize the mass of the structure where it most influences the efficiency of the design. That runs counter to the simple approach. Instead, I thought of the bridge as a system of two cantilevering beams. This type of layout places the greatest cross-section size over the abutments.

Cantilever bridges were once very common, owing to the ability to construct out from the piers until meeting in the middle. This reduced or eliminated the need for temporary piers or barges located in the deepest part of the body of water below. Employing such a construction method would be advantageous in this example as well, so that the marina below could remain in operation to the fullest extent possible.

Before I could run some preliminary numbers, I needed to make several estimates about the size and scope of the project. From Google maps, I estimated a free span of 600 ft. Taking all of the abutment requirements into account the real span might be a fair distance larger, but this estimate provides a baseline for exploring the concepts. Secondly, I estimated from the architectural sections, the dimensions of the superstructure. The platforms looked to be about 25 ft wide. The total height might be 45 ft. at the maximum depth. Since the exterior shape was to be comprised of many jagged surfaces, I applied a 33% reduction of the height to approximate the relative location of the main structural elements, treated as two lumps of steel - one representing the top chord of a truss, and the other the bottom chord.

I could estimate the weight of the bridge by taking the lumped mass of steel plus another 50% to account for connections, web members and cladding. Depending on the type of façade and the interior build-out, that number could be substantially larger. For the live load, due to pedestrians and amenities, I applied the 100 PSF load stipulated by the CBC for corridors, lobbies and other public space. Notably missing from my quick calculations were allowances for the effects of mother nature. Snow accumulation and lateral wind pressures would place a particularly large demand on any actual structure.

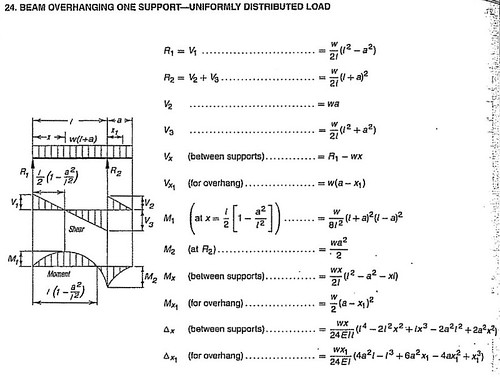
Nevertheless, I proceeded with a basic cantilever model. With the inputs described above, I was able to use pre-derived equations (taken from the AISC Steel Manual) to estimate the deflection of the beam at it’s cantilevered end and the amount of moment accumulated above the piers. As expected for such a long span, the deflections were large. Use of the spreadsheet allowed me to incrementally increase the amount of structural steel until arriving at quantity that seemed to meet the criteria. Again using my building background, I sought a deflection of no more than the length of the span divided by 360 (an arbitrary, but typically justifiable criteria). A deflection due to live loads up to 20 in. would be acceptable.

I also experimented with the length of the back-span. Intuitively, I figured that the longer the back-span, the smaller the end displacements. However, since my simple equation assumed the same stiffness throughout the length of the beam, when the back-span length increased too much, it became too flexible to provide a steady prop for the cantilever. This suggests that the architectural concept, which shows a short but deep section behind the forward pier, conceptually meets the structural demand.

After iterating through my calculations to meet deflection and strength criteria, I arrived at a design that called for about 1200 tons of structural steel. In more graphic terms, the bridge truss superstructure would consist of thirteen 14 in. wide flange beams (I-shaped) each weighing about 120 pounds per foot. Considering the other factors left out of my analysis, this seemed like an expensive brute force way to achieve the design.

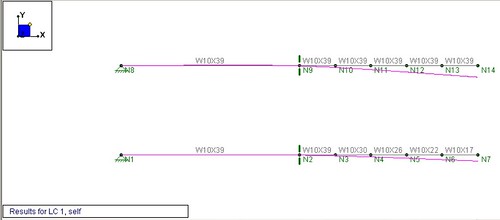
I thought back to the original intent to minimize structural mass where not required by strength demands. The simple model assumed that the entire length of the bridge consisted of the same size section. However, because we chose a cantilevered design, the forces in the members would decrease as we approached the end of the cantilever. The structural shape could also taper with that demand. I used RISA 2D, a simple finite element analysis program, to compare the effect of tapered versus constant sections. In the tapered model, I reduced the weight of the section by 60% from the pier to the free end. As a baseline to see if I was still meeting the strength and stiffness minimums, I computed the deflection due to a constant live load first. The results showed an almost negligible difference. The effect on the dead load deflection, however, was a significant 50% reduction.

These results indicated that the original design had been conceived with sound structural principles in mind. Of course, many issues still remain to be addressed. One such concern is whether the multi-faceted shell will be stable. The jagged exterior form seems to call for some type of internal space frame or self-bracing mechanism to prevent the perimeter from buckling. Surely solutions exist, but a what cost to the overall project.

Without even addressing many additional design considerations, the steel quantities that I had arrived at still seemed heavy. Perhaps more efficiencies could be realized without compromising the architecture. Looking for inspiration, I would turn to other bridge examples. In the form of suspension bridges, I remembered the principles of catenary structures. To be continued in the next post…

How would you have conducted this schematic evaluation? Do you agree with the load applied? Would you have used the full section depth to estimate the building stiffness? What other important considerations were ignored in this evaluation?

Will new faces deliver landmarks?

Early in 2009, Chicago’s architecture community was a buzz about the opportunity to design spaces for the 2016 Olympics. They looked to showcase the city’s rich architectural history and implement new modern forms being explored by a new generation of architects. Adina Balasu was one such enterprising designer completing her graduate degree. As part of her studies, she devised a landmark bridge to allow pedestrians access Olympic venues on Northerly Island, just across the marina from Soldier Field.

The concept, christened Chameleon, was to create a functional bridge that would be a destination in itself. Two levels of walkway would be suspended within a futuristic space frame shell. The large interior space might also be used as a multi-purpose venue for entertainment, retail and relaxation. After the Olympics left, the structure would be a necessary link to further the planned development of the little-used island park. An inspirational form and engineering feat, visitors would make a visit to the Chameleon part of their itinerary, expanding the traditional Chicago tourist district several blocks south.

I was introduced to the project at a meeting of the AIA Young Architects Forum. Following Ms. Balasu’s presentation, we had the opportunity to discuss the details of the project. I was intrigued by the structural challenge and impressed with her desire to express the structural form in the bridge’s appearance to reflect the technology of the times.

I delayed in my review for several months before picking up the concept with a fresh perspective. Unfortunately, in that time, Chicago was passed over for the Olympic bid. Despite this missed opportunity, I started wondering who deliver the trend-setting designs of the future. The current recession seems to have stalled several major projects, and missing out on the Olympics further deflated the local architecture community. When the economy turns around again, who will be at the forefront. I suspect that many of the innovative architects that I met at the YAF will lead the charge.

The Chameleon appeals to me as one of those great next-generation architectural concepts. Over the next few blogs I will outline my thought process and presents some potential strategies for making the Chameleon stand.

What do you think, when will we escape the current economic downturn? Will their be a new generation of architects leading the way at that time? Where should enterprising structural engineers look to network with these future partners? Please comment below.